Parallelizing Monte Carlo Simulation

🏆 This feature requires compute resources

MecSimCalc supports multiprocessing when higher compute resources are chosen. For more information, visit the code optimization page.

Overview

The Monte Carlo Simulation can be parallelized by implementing multiprocessing. This can significantly enhance the speed of the Monte Carlo Simulation.
Note: This only applies to greater than 2 vCPUs and requires subscription to higher compute resources on MecSimCalc.

Here is a comparison in the time the program takes to run between using multiprocessing and running the program serially in a simple Monte Carlo Simulation program with O(n) time complexity:

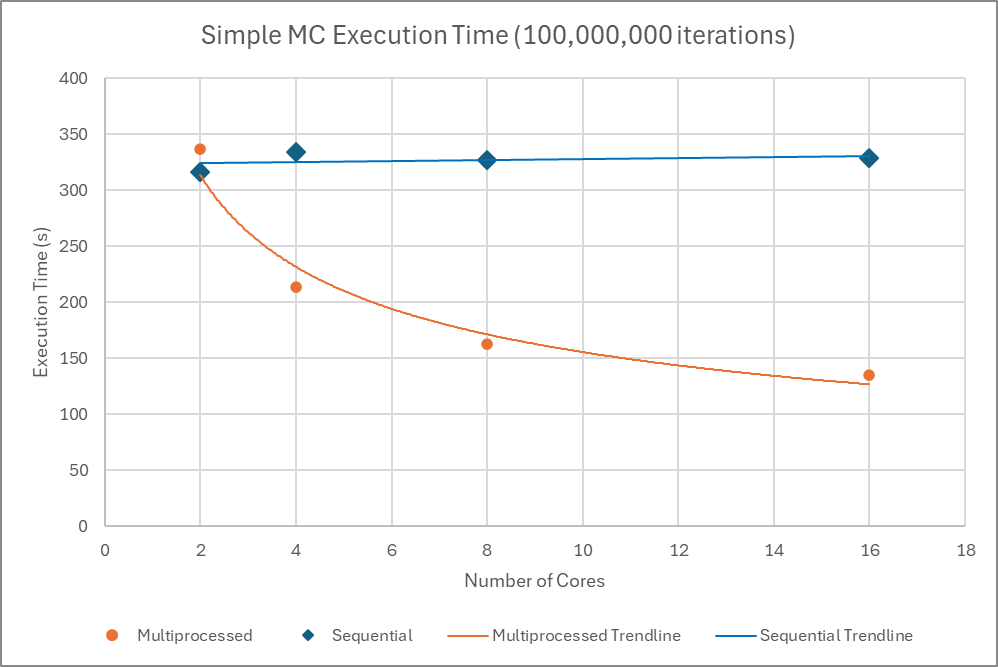
Multiprocessing will exponentially reduce the time taken to run the program as the number of CPU cores increase, whereas the execution time remains constant without multiprocessing.

Here is another comparison between sequential and parallel execution time in a computationally heavy Monte Carlo Simulation program used to determine strain demand in pipes subject to ground movement. More details can be found here.
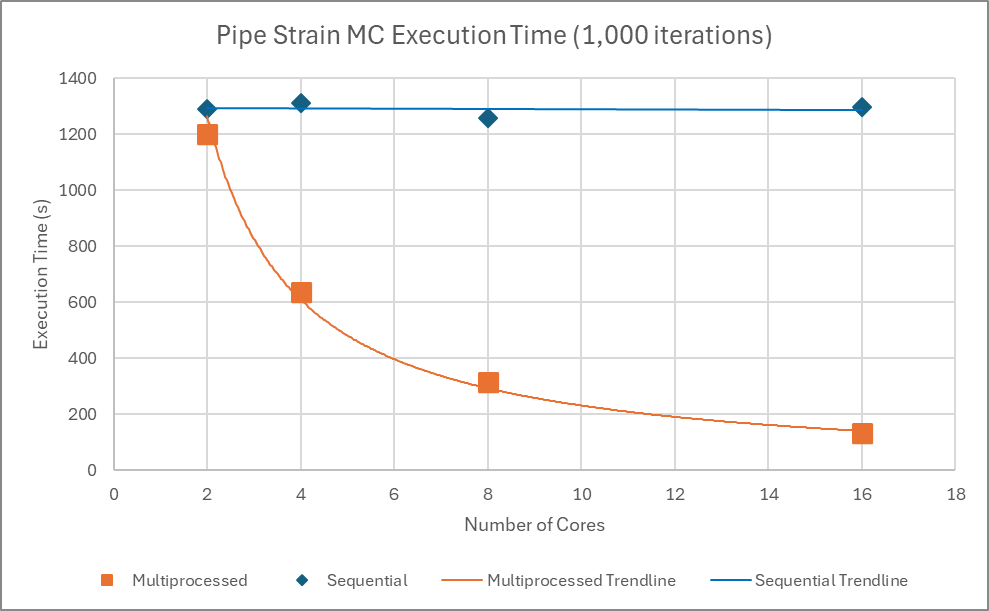
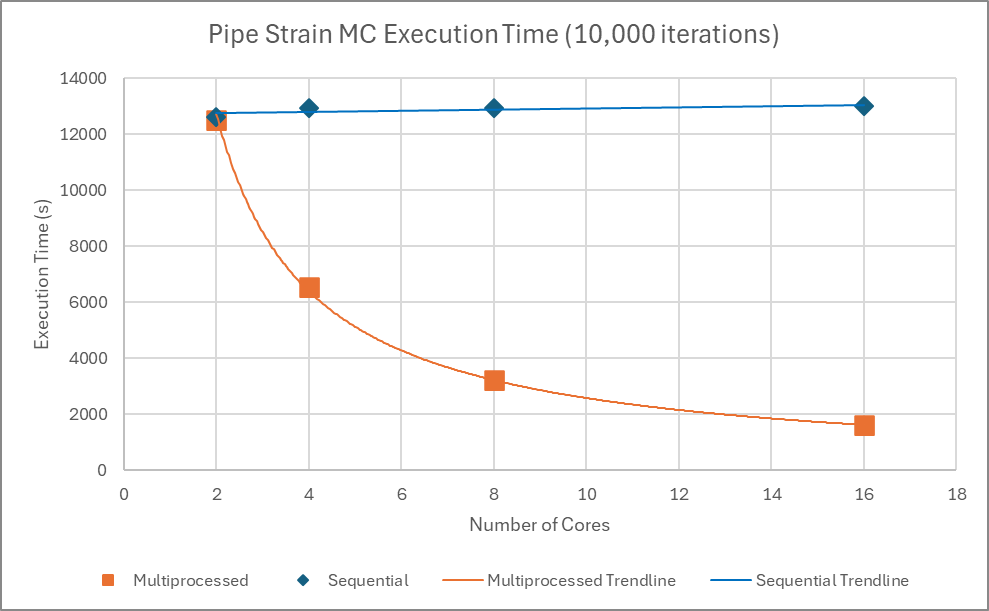Similar to the previous example, parallelization consistently reduces program execution time as CPU cores increase regardless of the number of simulations.

Implementing Multiprocessing

This tutorial requires a working Monte Carlo simulation program implemented on MecSimCalc. For more information on how to port your Python program to MecSimCalc, visit Getting Started.

There are multiple ways to implement multiprocessing and the methods shown may not work for all programs. Use these instructions as a rough guide.

1. Modularize the Program
   Arrange the program into functions so there is one function that runs the simulation. This will make it easier to implement multiprocessing.

2. Import the Multiprocessing Module

import multiprocessing

3. Create a Shared Object
   An object with shared memory between the processes will be required to store any function return data. The shared object can be any data type and must be created in main. This can be done using the manager object from the multiprocessing module.

   The example below creates a list with shared data that can be accessed between all processes.

def main(inputs):
    ### Other Code
    manager = mp.Manager() # This is case-sensitive
    data = manager.list()
    ### Other Code

4. Count the Number of CPU Cores This step can be skipped for those who want a specific number of processes. Otherwise, we can use this to count the optimal number of processes.
   Note: the number of CPU cores is dependent on the selection of vCPUs in MecSimCalc

def main(inputs):
    ### Other Code
    num_cores = multiprocessing.cpu_count()
    ### Other Code

5. Divide Tasks Among Each Process In the following example, the simulation is repeated num_simulations number of times.

def split_list(lst, n):
    k, m = divmod(len(lst), n)
    return (lst[i*k+min(i, m):(i+1)*k+min(i+1, m)] for i in range(n))

def main(inputs):
    ### Other Code
    arr = range(num_simulations)
    simulations_per_process = list(split_list(arr, num_cores))
    num_processes = min(num_cores, num_simulations)
    ### Other Code

6. Create the Processes
   Create processes by using a for loop to iterate over the number of processes you have determined in step 4 and 5. In this example, simulation() is the function to run the simulation and is used to create each process by setting target=simulation. simulation_args is a placeholder for any other arguments the simulation() function requires.

def main(inputs):
    ### Other Code
    processes = []
    for i in range(num_processes):
        # Create the process
        p = mp.Process(target=simulation, args=(simulations_per_process, simulation_args))
        processes.append(p) # Add the process to the list of processes
        p.start() # Starts the process
    for p in processes:
        p.join()
        # This waits for other processes to finish executing before continuing
    ### Other Code

Sample Implementation of Multiprocessing

The following is a Monte Carlo Simulation of a simple dice game adapted from here.

• Each player starts with $1000
• When the two dices rolls the same number, the player gets 4 times their bet amount
• If the dices do not roll the same number, the player loses their bet

The following Monte Carlo Simulation divides each simulation into max_num_rolls number of dice rolls, and repeats the simulations num_simulations times.

Before Implementing Multiprocessing

import matplotlib.pyplot as plt
import random
import time
import mecsimcalc as msc

def roll_dice():
    die1 = random.randint(1,6)
    die2 = random.randint(1,6)

    if die1==die2:
        same_num = True
    else:
        same_num = False
    return same_num

def simulate(num_simulations, max_num_rolls, bet):

    win_probability = []
    end_balance = []
    results = []

    for _ in range(num_simulations):
        balance = [1000]
        num_rolls = [0]
        num_wins = 0

        while num_rolls[-1] < max_num_rolls:

            if roll_dice(): #If both dices roll the same number
                balance.append(balance[-1] + 4 * bet)
                num_wins += 1

            else:
                balance.append(balance[-1] - bet)

            num_rolls.append(num_rolls[-1] + 1)

        win_probability.append(num_wins/num_rolls[-1])
        end_balance.append(balance[-1])
        results.append([num_rolls, balance])

    # Tracking variables
    overall_win_probability = sum(win_probability)/len(win_probability)
    overall_end_balance = sum(end_balance)/len(end_balance)

    return results, overall_win_probability, overall_end_balance

def main(inputs):
    start = time.time()

    # Inputs
    num_simulations = inputs['num_simulations']
    max_num_rolls = inputs['max_num_rolls']
    bet = inputs['bet']

    # Simulation
    results, overall_win_probability, overall_end_balance = simulate(num_simulations, max_num_rolls, bet)

    # Plotting
    plt.figure()
    plt.title("Monte Carlo Dice Game [" + str(num_simulations) + " simulations]")
    plt.xlabel("Roll Number")
    plt.ylabel("Balance [$]")
    plt.xlim(0, max_num_rolls)

    for result in results:
        num_rolls, balance = result
        plt.plot(num_rolls, balance)

    end = time.time()

    elapsed_time = end - start

    img, download = msc.print_plot(plt, download=True)

    return {
        "plot": img,
        "download": download,
        "time_taken": elapsed_time,
        "win_prob": overall_win_probability,
        "end_bal": overall_end_balance
    }

After Implementing Multiprocessing

import matplotlib.pyplot as plt
import random
import time
import multiprocessing as mp
import mecsimcalc as msc

# Rolls the dices and checks if they are the same number
def roll_dice():
    die1 = random.randint(1,6)
    die2 = random.randint(1,6)

    if die1==die2:
        same_num = True
    else:
        same_num = False
    return same_num

def simulate(num_simulations, max_num_rolls, bet, shared_list):

    for _ in range(num_simulations):

        balance = [1000]
        num_rolls = [0]
        num_wins = 0

        while num_rolls[-1] < max_num_rolls:
            if roll_dice(): #If both dices roll the same number
                balance.append(balance[-1] + 4*bet)
                num_wins += 1

            # Result if the dice are different numbers
            else:
                balance.append(balance[-1] - bet)

            num_rolls.append(num_rolls[-1] + 1)

        # Tracking variables
        win_probability = num_wins/num_rolls[-1]
        end_balance = balance[-1]
        shared_list.append([num_rolls, balance, win_probability, end_balance])
        #Return by appending to shared list

    return # Function return must be null

def split_list(lst, n):
    k, m = divmod(len(lst), n)
    return (lst[i*k+min(i, m):(i+1)*k+min(i+1, m)] for i in range(n))

def main(inputs):
    start = time.time()

    # Inputs
    num_simulations = inputs['num_simulations']
    max_num_rolls = inputs['max_num_rolls']
    bet = inputs['bet']

    # Plotting
    plt.figure()
    plt.title("Monte Carlo Dice Game [" + str(num_simulations) + " simulations]")
    plt.xlabel("Roll Number")
    plt.ylabel("Balance [$]")
    plt.xlim(0, max_num_rolls)


    ### Multiprocessing

    # Create shared list between processes
    manager = mp.Manager()
    results = manager.list()

    # Count the number of CPUs
    num_cores = mp.cpu_count()

    # Divide the tasks (number of simulations) for each process
    arr = range(num_simulations)
    simulations_per_process = list(split_list(arr, num_cores))
    num_processes = min(num_cores, num_simulations)

    # Create the processes
    processes = []
    for i in range(num_processes):
        p = mp.Process(target=simulate, args=(len(arr_partitions[i]), max_num_rolls, bet, results))
        processes.append(p)
        p.start()

    for p in processes:
        p.join()

    ###

    overall_win_probability = 0
    overall_end_balance = 0

    for result in results:
        num_rolls, balance, win_probability, end_balance = result
        overall_win_probability += win_probability
        overall_end_balance += end_balance
        plt.plot(num_rolls, balance)

    overall_win_probability /= len(results)
    overall_end_balance /= len(results)


    end = time.time()
    # Averaging win probability and end balance

    elapsed_time = end - start

    img, download = msc.print_plot(plt, download=True)

    return {
        "plot": img,
        "download": download,
        "time_taken": elapsed_time,
        "win_prob": overall_win_probability,
        "end_bal": overall_end_balance,
        "cpu_count": num_processes
    }